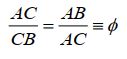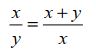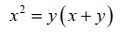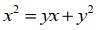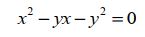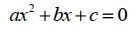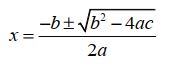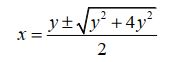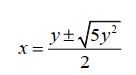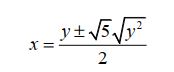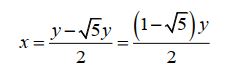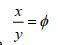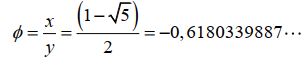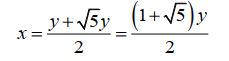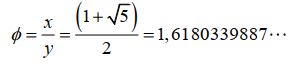Anderson Lupo Nunes ***
Introdução
A Maçonaria possui um simbolismo oculto, o qual o irmão deve se debruçar no estudo e meditação acerca do aspecto ritualístico para desvendar o seu significado. Há, de certa forma, uma Maçonaria velada e que nem todos os irmãos têm acesso. Isto é natural, pois apesar de toda a abertura do conhecimento e o aprimoramento dos meios de comunicação, a Maçonaria continua sendo profundamente mística e esotérica. Efeitos psicológicos acerca do simbolismo maçônico são apresentados em Guimarães (2013).
Segundo Janotta (2013), boa parte do simbolismo maçônico é fundamentado no Templo de Salomão, apresentado na Bíblia Sagrada (2012) em Êxodo cap. 26 até 29 como uma tenda que deveria abrigar o Senhor durante a peregrinação dos judeus que eram guiados por Moisés até a Terra Santa. Com a sua fixação na região da Palestina, houve uma época de muitos conflitos que se acentuaram durante o reinado de Davi. Após a sua morte sobe ao trono o seu filho, Salomão. Segue-se um período de paz e prosperidade, que o motivou a construir o Templo de Deus na Terra Prometida, de acordo com I Reis no capítulo 1 e capítulos 5 até 7.
Buchanan (2013) realiza uma busca arqueológica ao Templo de Salomão contestando o senso comum de que ele ficava originalmente na Cúpula da Rocha, afirmando que quando foi totalmente destruído pela primeira vez em 516 A.C. ele ficava perto da fonte de Siloé. A importância dessa busca reside no fato de que o Templo não é apenas simbólico e mitológico, mas também uma realidade histórica inserida em um contexto atual sócio-político bastante complexo.
A construção do Templo de Salomão começou no ano 480 após o êxodo, segundo I Reis, cap. 6 vers. 1 e levou um período de 13 anos até o término da obra. Segundo Durão (2003), Salomão era um grande artista e um alquimista, tendo desenhado a maior parte dos enfeites do Templo e também teria manufaturado, por meios alquímicos, parte do ouro utilizado na sua construção. Vale ressaltar a carência de referências nas afirmativas de Durão (2003). Ismail (2012) ressalta que a Maçonaria sempre teve uma relação com o Templo de Salomão. Adoum (1972) trata de aspectos simbólicos do Tabernáculo no deserto que seria o símbolo do corpo físico no deserto da matéria. O Tabernáculo, ou o corpo físico, foi dado ao homem para que ele encontre Deus. Williams (2004) também destaca os mesmos aspectos relatados por Adoum (1972) e ainda trata de relações com os sólidos platônicos e os chakras.
A proposta do presente trabalho consiste em relacionar aspectos simbólicos do Templo de Salomão com a sequência de Fibonacci. O manancial de símbolos acerca de ambos é muito rico e a interseção entre eles é a matéria prima desta obra. A relevância do tema se justifica pela importância dos aspectos simbólicos relacionados. A sequência de Fibonacci aparece nas mais diversas manifestações da vida no planeta Terra. Da quantidade de pétalas das flores até as espirais do caracol e da própria via Láctea são alguns exemplos de aplicação desta sequência.
Uma notável descoberta revelada por Tattersall (2013) consiste no fato de que os períodos das órbitas de todos os planetas o sistema solar, incluindo os dois planetas anões, possui uma estreita correspondência com os vinte primeiros termos da sequência de Fibonacci. O erro médio entre os vinte e oito pontos de dados é demonstrado estar sob 2,75%.
Um número que surge naturalmente no estudo matemático da sequência de Fibonacci é a chamada Razão Áurea, também chamada de Divina Proporção ou mesmo Proporção Áurea. O seu estudo é relevante para este trabalho.
A Razão Áurea
Trata-se de um número irracional que pode ser obtido a partir de certas proporções do ser humano e da Natureza em geral. Por unir macrocosmo e microcosmo assume um aspecto divino, daí também ser conhecido como Divina Proporção. Existe mais de uma maneira de deduzir a Razão Áurea, conforme pode-se verificar em Queiroz (2010), Conte (2008) e Lawor (1997). Na verdade usarei um método pessoal, partindo dos conceitos apresentados nas três referências.
Considere um seguimento de reta definido pelos pontos A e B abaixo: Marque um ponto C qualquer entre A e B.
Marque um ponto C qualquer entre A e B. Tanto faz se o ponto está mais próximo de A ou de B.
Quando a razão (divisão) entre o maior trecho (AC) e o menor trecho (CB) é igual a divisão entre o seguimento de reta completo (AB) e o maior trecho (AC) o resultado da divisão é um número irracional chamado de Divina Proporção ou Razão Áurea. Matematicamente a afirmativa acima pode ser escrita:
A letra grega 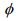 (Phi) representa a própria Razão Aurea. Para deduzir o valor de
(Phi) representa a própria Razão Aurea. Para deduzir o valor de 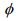 , vamos chamar o trecho AC de x e o trecho CB de y. A equação acima pode ser reescrita:
, vamos chamar o trecho AC de x e o trecho CB de y. A equação acima pode ser reescrita:
Multiplicam-se os denominadores cruzados pelos numeradores:
Em seguida, aplica-se a propriedade distributiva ao termo da direita:
O termo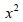 passa para o lado esquerdo da equação:
passa para o lado esquerdo da equação:
A equação acima, considerando o x como a incógnita, torna-se uma equação do segundo grau.
Note que se escolhêssemos o y como incógnita a equação seria exatamente a mesma. Foi por conta desta simetria que afirmei acima que tanto a menor distância ser AC ou CB. A equação do segundo grau é resolvida pela fórmula de Báscara.
Aplicando a fórmula de Báscara à equação 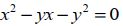 , segue:
, segue:
É possível simplificar a equação acima. Primeiro, soma-se os termos de dentro da raiz quadrada.
Segundo, aplica-se a propriedade do produto de raízes:
Seguem duas opções de simplificações para a equação. A primeira é:
Este resultado é falso uma vez que x e y são positivos e assim a Razão Aurea não pode ser negativa. Resta, portanto a outra alternativa:
Logo,
O número 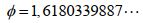 é chamado de Razão Áurea ou Divina Proporção. É irracional porque resulta de uma divisão em que o resultado não é exato, ou seja, após infinitas etapas de divisões o resto nunca se anula. O seu simbolismo é muito rico, o infinito presente no finito, o eterno expresso e limitado no tempo.
é chamado de Razão Áurea ou Divina Proporção. É irracional porque resulta de uma divisão em que o resultado não é exato, ou seja, após infinitas etapas de divisões o resto nunca se anula. O seu simbolismo é muito rico, o infinito presente no finito, o eterno expresso e limitado no tempo.
Aspectos naturais da Razão Áurea
A Divina Proporção está presente em diversas relações do corpo humano, segundo Queiroz (2010) e Melchizedek (2009): ·
- A altura do corpo e a medida do umbigo até o chão.
- A medida da cintura até a cabeça e o tamanho do tórax
- O tamanho dos dedos e a medida da dobra central até a ponta.
- A altura do crânio e a medida da mandíbula até o alto da cabeça.
- A medida do quadril ao chão e a medida da mandíbula até o alto da cabeça.
Também encontramos a Razão Áurea no comportamento da refração da luz, nos átomos, nas espirais das galáxias, nas ondas dos oceanos, nos furacões. Ela já era conhecida dos antigos egípcios que construíram suas pirâmides utilizando a Divina Proporção nos blocos de pedra e nas câmaras internas de seus monumentos.
Segundo Melchizedek (2009) as dimensões da Razão Áurea no corpo humano nunca são exatas em uma pessoa. Quando um bebê nasce o seu umbigo se situa exatamente no centro geométrico do corpo. À medida que a criança cresce a posição do umbigo começa a se mover na direção da cabeça até chegar exatamente na Razão Áurea, mas continua subindo. Depois vai descendo e assim, sucessivamente, oscilando em torno da posição correspondente à Divina Proporção. Quando chega a idade adulta se estabiliza em um ponto um pouco acima ou abaixo da Proporção Áurea, na maioria dos homens ligeiramente acima e na maioria das mulheres ligeiramente abaixo. Na média da humanidade fica exatamente no ponto correspondente à Razão Áurea. Lawor (1997) também cita a oscilação da posição do umbigo em relação à Razão Áurea e o fato de que nos homens é acima e nas mulheres, abaixo.
Lawor (1997) afirma que a Proporção Áurea é uma razão constante derivada de uma relação geométrica que tal qual o π e outras constantes deste tipo é irracional em termos numéricos. Acima de tudo deve ser apresentada como uma proporção sobre a qual se funda a experiência do conhecimento. Assim, a Proporção Áurea pode ser considerada como suprarracional ou transcendental.
Foi Pitágoras, segundo Conte (2008), quem descobriu que a Razão Áurea representava uma lei biológica que regula o crescimento de todas as coisas vivas. Chegou a esta conclusão ao medir e analisar uma belíssima concha marinha (Nautilus pompilius), bastante comum nas praias da ilha de Samos.
Mas Pitágoras tinha a convicção de que a Natureza era regida pelo número quatro. Assim, pode representar a perfeição da espiral da concha por uma sequência de quadrados, começando com um quadrado de lado igual a um e ajustando os quadrados seguintes ao crescimento da espiral. O mesmo exercício geométrico feito com a perfeita espiral de uma concha pode ser feito com a Via Láctea. Esta sequência numérica é muito especial e parece ser a chave para explicar a Razão Áurea.
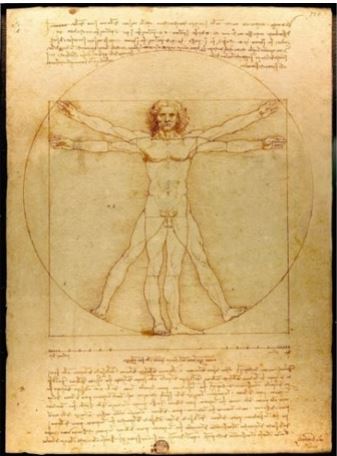
Figura 1: Homem de Vitruvio de Da Vinci (1485-90, Veneza)
A Sequência de Fibonacci
Leonardo Da Vinci se notabilizou, entre diversas outras obras, por um esboço chamado de o Homem Vitruviano ou Homem de Vitrúvia, apresentado na Figura 1. Melchizedek (2009) e Lawor (1997) comentam que é possível traçar uma espiral sobre o desenho que tem uma importante relação com Razão Áurea. A espiral é construída a partir de um quadrado 1×1, seguido de outro quadrado idêntico. Os dois primeiros quadrados formam o lado do terceiro quadrado 2×2 e assim sucessivamente. A Razão Áurea presente no esboço de Da Vinci revela a espiral abaixo feita pelos lados sucessivos de quadrados, formando a sequência de Fibonacci.
Figura 2: A Espiral de Fibonacci
A sequência numérica presente na espiral da figura 2 foi revelada por Leonardo Fibonacci (11701250) em sua obra Liber Abaci, embora não tenha sido ele que descobriu a sequência, ela recebeu o seu nome após a sua morte. Fibonacci foi o primeiro e um dos mais importantes matemáticos europeus da Idade Média, segundo Eves (1990).
Considere o número 1, representa o Todo, o Grande Arquiteto do Universo. Ele cria uma imagem de si mesmo, ou seja, outro número 1. Soma-se os dois primeiros números da sequência o que resulta no 2. Soma-se o 2 com o anterior o que resulta o 3. Repete-se sempre a soma do número com o anterior sucessivamente e obtém-se a Sequência de Fibonacci.
1 1 2 3 5 8 13 21 34 55 89…
A sequência de Fibonacci apresenta muitas propriedades que, segundo Kalman & Mena (2003), podem ser classificadas como maravilhosas. As somas ou as diferenças entre números da sequência de Fibonacci resultam em números que também são da sequência. Quaisquer quatro números seguidos de Fibonacci podem ser combinados para formar um terno pitagórico, ou seja, dos quatro números é possível tirar três que formam os catetos e a hipotenusa de um triângulo retângulo (onde vale o Teorema de Pitágoras). Estas e outras propriedades da sequência de Fibonacci são descritas por Kalman & Mena (2003) com maiores detalhes.
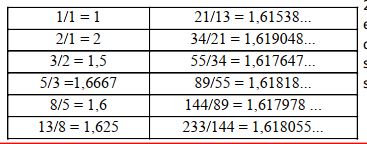
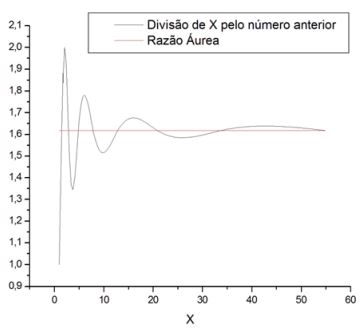
A relação entre a Sequência de Fibonacci e a Razão Áurea é bastante simples. Basta dividir um número da sequência pelo seu antecessor. Quanto maior for o número, mais o resultado se aproxima da Razão Áurea. Vejamos a seguinte tabela:
Tabela 1: Termos consecutivos da sequência de Fibonacci convergindo para a Razão Áurea
Representando a aproximação da divisão dos termos seguidos em relação à Razão Áurea observa-se um comportamento oscilatório, que já havia sido comentado neste trabalho por meio do exemplo sobre a posição do umbigo do bebê até chegar à idade adulta. Observe o comportamento oscilatório no gráfico da Figura 3.
Figura 3: Gráfico que mostra a oscilação dos termos da sequência de Fibonacci em torno da Razão Áurea produzido pelo autor no aplicativo Microcal (TM) Origin versão 6.0
A sequência de Fibonacci, vinculada à Razão Áurea, está associada a uma miríade de fenômenos biológicos, atômicos e estelares. Melchizedek (2009) mostra a presença da sequência na quantidade de pétalas das flores, a distribuição das folhas e das sementes. Também aparece nas espirais presentes na anatomia humana, nos caracóis, etc. Tashtoush & Darwish (2012) utilizam a sequência de Fibonacci na construção de um protocolo que melhora em até 21% a transmissão dos dados em uma rede. Mishra et al. (2012), por sua vez, utilizam a sequência para criar um novo modelo de criptografia de imagem. A sequência de Fibonacci revela uma ordem natural subjacente a todo o Universo.
Relações com o Templo de Salomão
A Maçonaria revela aspectos simbólicos do Templo de Salomão que são velados e segundo minha análise e inspiração tem uma relação direta com a sequência de Fibonacci, e por contiguidade, à Razão Áurea. Morrison (2008) revela a metáfora arquitetônica do Templo de Salomão correlacionando sua geometria com o corpo humano e demais elementos naturais a partir do estudo acerca de uma obra de Juan Battista Villalpando publicada em 1604.
O início do ingresso no Templo de Salomão se faz pela antessala, que pode ser simbolizada pelo número 1, é Princípio no sentido cosmogônico do termo, portanto, o início da sequência de Fibonacci.
Queiroz(2010), Melchizedek (2009) e Lawor (1997) relacionam o simbolismo do número 1 à unidade e ao princípio organizador do Universo. Goswami (2007) afirma que a consciência necessária, segundo uma interpretação idealista da Física Quântica, é única.
Um referencial absoluto e necessário para que todo o Universo se manifeste. Na verdade ele adota o conceito de mônada, criado por Leibnitz e o amplia, definindo a mônada quântica.
O Aprendiz Maçom está ainda no pavimento térreo do Templo do Rei Salomão, segundo Adoum (1972). Este pavimento simboliza o próprio Aprendiz e é o reflexo do princípio. Logo é o segundo termo da sequência de Fibonacci, ou seja, o segundo 1. Na Bíblia Sagrada (2012), Livro da Gênesis, cap. 1 vers. 26 está escrito: “Deus disse: Façamos o ser humano a nossa imagem e segundo nossa semelhança,(…)” A consciência humana é um reflexo da consciência cósmica. Este ponto do estudo é relevante porque se do Princípio não surgisse a sua imagem ou reflexo não existiria a Criação. Se não fosse o surgimento do segundo 1 na sequência de Fibonacci ela simplesmente não existiria. Hurtak (1996) afirma que o Homem é feito na imagem e similitude, onde o “na” indica que a evolução é um contínuo assimilar de Luz. Ubaldi (1999) que cada fenômeno só existe porque há movimento de um ponto de partida para um ponto de chegada. O surgimento do segundo número 1 da sequência de Fibonacci mostra, portanto, o primeiro movimento da Criação.
O aprendiz no início de seu movimento para o pavimento superior do Templo de Salomão fica entre as duas colunas, B. e J., que juntas elas dão a ideia da dualidade. Simbolizam o terceiro termo da sequência de Fibonacci, ou seja, o número 2. Na Bíblia Sagrada (2012), Livro da Gênesis, cap. 1 vers. 27 está escrito: “Deus criou o ser humano à sua imagem, à imagem de Deus o criou, macho e fêmea ele os criou.” Note que é só no cap. 2, vers. 21, 22 e 23 que está escrito que Deus criou a mulher a partir da costela de Adão.
Qual seria então o significado da afirmativa que Deus criou o ser humano, à sua imagem, macho e fêmea? Parece ser uma referência ao princípio de Dualidade.
Na Bíblia Sagrada (2012), Livro I Reis , cap. 6 vers. 21 trata da construção do Templo de Salomão, onde aparece a figura do artífice Hiram Abiff que teria construído as colunas. Está escrito: “Em seguida ele ergueu as colunas na frente do vestíbulo do templo: levantou a coluna do lado direito dando o nome de Jaquin; em seguida levantou a coluna do lado esquerdo, chamando-a de Booz.” A seguir, vem a escada em forma de caracol.
Note que o caracol, por si só é uma referência a Pitágoras e o formato perfeito das conchas que tanto inspiraram esse Venerável Mestre. Os três primeiros degraus aludem ao princípio ternário, representado no altar pelas Três Grandes Luzes da Maçonaria. Representam também as virtudes Sabedoria, Força e Beleza. É cabível também uma relação com os pilares da Árvore da Vida, segundo Marques (2011). Chega-se ao quarto termo da sequência de Fibonacci, o número 3.
Os cinco degraus seguintes representam às cinco ordens clássicas da Arquitetura, ou seja, Dórica, Jônica, Coríntia, Toscana e Compósita. As informações acerca da Arquitetura Clássica foram preservadas através da obra de Vitrúvio, que viveu no século I A.C. , segundo Maciel (2009). Aludem também aos cinco sentidos humanos e aos cinco elementos alquímicos, a saber, Terra, Ar, Água, Fogo e Éter. Uma descrição sucinta dos cinco elementos alquímicos é feita por Cotnoir & Wsserman (2009), que relacionam o quito elemento com o campo, ou seja, a fonte de tudo o que existe. Nota-se que a referência às cinco colunas da Arquitetura Clássica passam uma ideia de ordem ou mesmo simetria, conceito fundamental da Razão Áurea. Surge o quinto termo da sequência de Fibonacci, o número 5.
Em seguida vem sete degraus que aludem a todo o simbolismo do número sete. Os sete dias da semana, as sete cores do arco-íris, os sete planetas, os sete orbitais atômicos, as sete notas musicais, entre outros, são aspectos naturais relacionados ao número sete segundo Marques (2011) e Queiroz (2010).
Os sete degraus simbolizam as sete artes ou ciências liberais: Gramática, Retórica, Lógica, Aritmética, Geometria, Música e Astronomia. As três primeiras, ou seja, Gramática, Retórica e Lógica, eram as disciplinas da Universidade conhecidas como Trivium e que tinham como objetivo o provimento da mente para encontrar expressão na linguagem, segundo Joseph (2008). Ainda em Joseph (2008), as quatro últimas, ou seja, Aritmética, Geometria, Música e Astronomia, eram conhecidas como Quadrivium e o seu objetivo era o provimento de meios para o estudo da matéria.
Mas eis que surge um problema, o sexto número da sequência de Fibonacci é 8 e não 7. Mas imagine, ao terminar de subir os sete degraus o Aprendiz chega à câmara do meio do Templo do Rei Salomão. O término da escada não é no sétimo degrau, e sim no próprio piso da câmara do meio. São oito passos, portanto. Mas haveria um simbolismo para o piso da câmara do meio? A câmara do meio é onde os obreiros recebem o pagamento. Nela observa-se a letra G. Poderia se pensar que a letra G representa a Geometria, mas esta ciência já foi verificada em um dos sete degraus.
Segundo Adoum (1972), desde os mais antigos rituais a letra G simboliza o Grande Arquiteto do Universo, merecendo, portanto, uma deferência especial. Assim, os sete degraus (sete ciências) somadas ao próprio Grande Arquiteto do Universo, simbolizam o número 8. Note que o número 8 simboliza o duas vezes quatro, a manifestação perfeita. O octanário é o número da realização da Divindade no Homem. Note que o oito é o símbolo do infinito voltado para cima. Chega-se ao sexto termo da sequência de Fibonacci, o número 8.
O que seriam das sete ciências sem a conexão com o Grande Arquiteto do Universo? Conclui-se com o sexto termo da sequência de Fibonacci. Segue com um quadro comparativo dos termos da sequência e seus aspectos relacionados ao Templo de Salomão, considerando o seu simbolismo.
Tabela 2: Termos da sequência de Fibonacci relacionados com o Templo de Salomão e o seu simbolismo

Considerações Finais
Todo o simbolismo do qual o presente artigo investiga encontra-se em um esquema que pode ser relacionado com diversos aspectos do macrocosmo e do microcosmo. Arola (1986) descreve diversos aspectos do simbolismo relacionado ao templo. Ismail (2012) também trata do simbolismo contido na Maçonaria, mostrando que nada está ali por acaso. Um símbolo pode ter tantos significados quantos sejam aqueles que dedicam ao estudo e meditação acerca do seu significado. Arola (1986) considera que o Templo é a interseção entre o Céu e a Terra, entre o Homem e Deus, porque um templo exterior e tangível é simplesmente o reflexo de um templo interior e intangível.
O Templo de Salomão apresenta aspectos de seu simbolismo que foram relacionados com os seis primeiros termos da sequência de Fibonacci. O próximo termo seria número 13 que por si só carrega todo um simbolismo. Foi em um dia 13 de Outubro de 1307 que Jacques de Molay foi preso, de acordo com Read (2001). A carta que representa a morte no Tarô Mitológico é exatamente a carta 13. Seu simbolismo está associado à transformação e a transmutação. Na Bíblia Sagrada (2012), Livro I Reis, cap. 7 vers. 1, está escrito: “Quanto ao palácio, Salomão levou treze anos para construí-lo de todo.” Note que a referência é ao palácio. No versículo anterior (I Reis, cap. 6, vers. 38) está escrito que o Templo levou sete anos para ser construído.
O fato de não ter encontrado relações do Templo de Salomão com o número treze não significa que tais relações não possam existir. Mas lembre-se que foram seis dias da Criação, e foram os seis primeiros termos da sequência de Fibonacci que foram relacionados com o Templo de Salomão. Ele simboliza tanto o microcosmo, representado pelo corpo humano, quanto o Universo, ou seja, o macrocosmo. A sequência deve terminar em algum dos termos.
É possível traçar mais relações entre o Templo de Salomão e a Cabala. Segundo Marques (2011), a Cabala é um sistema que permite compreender a similitude oriunda da unidade em todas as partes da Criação. É evidente que o Templo pode ser também esquematizado pelo viés da Cabala. A princípio todo modelo é incompleto e revela um ponto de vista acerca de um fato. Fica difícil definir qual seja o melhor. Isso não diminui a importância da comparação que foi feita com a sequência de Fibonacci. Pelo contrário, a sequência de Fibonacci ganha mais relevância com seus aspectos cabalísticos.
A existência de diversos artigos recentes relacionados à sequência de Fibonacci e ao Templo de Salomão demonstra que ambas as temáticas são atuais e inseridas em um contexto científico ou acadêmico. Guimarães (2013), Janotta (2013), Kalman & Mena (2003), Mishra (2012), Morrison (2008), Tashtoush & Darwish (2012) e Tattersall (2013) são exemplos de artigos recentes e que foram citados no presente artigo.
Conclui-se que o simbolismo acerca da sequência de Fibonacci é muito mais rico do que aparentava. O Grande Arquiteto do Universo transcende a mente e a compreensão humanas, mas seria possível ousar supor que a linguagem que está mais próxima da Mente Cósmica é a Matemática. Na Matemática está contida tudo o que existe, mas também o que não existe. Um exemplo de algo que não é mensurável na Natureza, mas existe na Matemática são os números complexos.
Ao traçar estas relações nossa mente se expande a vai de encontro à Mente Cósmica. Foi a partir daí que, segundo Conte (2008), Pitágoras concluiu estupefato: “Tudo no Universo são números”.
*** Anderson Nunes é Doutorando em Engenharia Nuclear pela UFRJ, Mestre em Engenharia Nuclear pela UFRJ, Especialista em Educação Tecnológica pelo CEFET-RJ, Graduado em Física pela UFRJ e em Formação Docente para o Ensino Fundamental e Médio pela Universidade Cândido Mendes. É membro da Loja de Pesquisas “Rio de Janeiro” – GOIRJ. E-mail: professorlupo@gmail.com
Referências Bibliográficas
ADOUM, Jorge. O Grau do Aprendiz e seus Mistérios. Ed. Pensamento-Cultrix, São Paulo, 1972.
AROLA, Ramón. O Simbolismo do Templo. Editora Objetiva, Rio de Janeiro, 1986.
BÍBLIA SAGRADA, Trad. Domingos Zamagna. Editora Vozes Ltda. 51a Ed., Petrópolis, RJ, 2012.
BUCHANAN, George Wesley. In Search of King Solomon’s Temple. Associates for Scriptural Knowledge. Portland, USA. Number 9/13, p. 30-35, September 2013.
CONTE, Carlos B.. Pitágoras, Ciência e Magia na Antiga Grécia. Editora Madras, São Paulo, 2008.
CORTNOIR, Brian e WASSERMAN, James. Introdução à Alquimia. Editora Pensamento. São Paulo, 2009.
DURÃO, João Ferreira. Pequeno Glossário de Filosofia, Esoterismo, História Antiga e Medieval. Editora Madras, São Paulo, NUNES, A. L. A SEQUÊNCIA DE FIBONACCI NO TEMPLO DE SALOMÃO FinP | Rio de Janeiro, Vol. 1, n.2, p. 21-30, Set/Dez, 2013. 30 2003.
GOSWAMI, Amit. O Universo Autoconsciente. Editora Aleph, São Paulo, 2007.
GUIMARÃES, Raphael. Os Efeitos Psicológicos da Prática do Ritual Maçônico. Revista Ciência & Maçonaria. Brasília, Vol. 1, n.1, p. 21-28, jan/jun, 2013.
HURTAK, J.J.. As Chaves de Enoch. Academia para Ciência Futura, São Paulo, 1996.
ISMAIL, Kennyo. Desmistificando a Maçonaria. Universo dos Livros, São Paulo, 2012.
JANOTTA, Rainer K.. Freemasons and the Symbol of the Building of King Solomon’s Temple. Pietre-Stones Review of Freemasonry. http://www.freemasons-freemasonry.com. Acesso em 28/10/2013.
JOSEPH, Miriam. O Trivium As Artes Liberais da Lógica, Gramática e Retórica. Tradução de Henrique Paul Dmyterko. Ed. Realizações. São Paulo, 2008 KALMAN, Dan & MENA, Robert. The Fibonacci NumbersExposed. Mathematics Magazine, VOL. 76, NO. 3, p. 167-181, JUNE 2003.
LAWOR, Robert. Geometria Sagrada. Edições Del Prado, Rio de Janeiro, 1997.
MACIEL, Manuel J. P. (Tradução do latim, Introdução e Notas).
Vitrúvio Tratado de Arquitetura. Ed. ISP Press. 3ª edição, Lisboa, 2009.
MARQUES, Hélio de Moraes e (coordenação e supervisão). A Cabala Desvendada. Biblioteca Rosacruz, Curitiba, 2011.
MELCHIZEDEK, Drunvalo. O Antigo Segredo da Flor da Vida, vol.1. Ed. Pensamento, São Paulo, 2009.
MISHRA, Minati, MISHRA, Priyadarsini, ADHIKARY, M.C. and KUMAR, Sunit. Image Encryption Using Fibonacci-Lucas Transformation. International Journal on Cryptography and Information Security (IJCIS),Vol.2, No.3, p. 131-141, September 2012.
MORRISON, Tessa. Juan Battista Villalpando: Solomon’s Temple and the Architectural Metaphor. The International Journal of the Humanities. Melbourne, vol. 6, number 1, p. 203-212, 2008.
QUEIROZ, Álvaro de. A Geometria Maçônica. Editora Madras, São Paulo, 2010.
READ, Piers Paul, trad. Marcos José da Cunha. Os Templários. Imago, Rio de Janeiro, 2001.
TASHTOUSH, Yahya M. and DARWISH, Omar A.. A Novel Multipath Load Balancing Approach Using Fibonacci Series for Mobile Ad Hoc Networks. International Journal of Computer Theory and Engineering Vol. 4, No. 2, p. 220-225, April 2012.
TATTERSALL, Roger. A remarkable discovery: All Solar system periods fit the Fibonacci series and the Golden Ratio. Why Phi? February 13 2013. http://tallbloke.wordpress.com/ Acesso em 28/10/2013.
WILLIAMS, Ani. The Sacred Geometry of Sound. The Spirit of Maat (digital review). Vol. 4, January, 2004. http:// http://www.spiritofmaat.com Acesso em 28/10/2013.
UBALDI, Pietro. A Grande Síntese. Editora Fraternidade Francisco de Assis, Rio de Janeiro, 1999
[1] Anderson Nunes é Doutorando em Engenharia Nuclear pela UFRJ, Mestre em Engenharia Nuclear pela UFRJ, Especialista em Educação Tecnológica pelo CEFET-RJ, Graduado em Física pela UFRJ e em Formação Docente para o Ensino Fundamental e Médio pela Universidade Cândido Mendes. É membro da Loja de Pesquisas “Rio de Janeiro” GOIRJ. E-mail: professorlupo@gmail.com
Publicada na Excelente revista FRATERNITAS IN PRAXIS Vol.1, Número 2, Set/Dez 2013